Monty halls problem.

Suppose you're on a game show and you're given the choice of three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed randomly behind the doors before the show. The rules of the game show are as follows: After you have chosen a door, the door remains closed for the time being. The game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two remaining doors, and the door he opens must have a goat behind it. If both remaining doors have goats behind them, he chooses one randomly. After Monty Hall opens a door with a goat, he will ask you to decide whether you want to stay with your first choice or to switch to the last remaining door. Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?" Is it to your advantage to change your choice? (Krauss and Wang 2003:10)

Note that the player may initially choose any of the three doors (not just Door 1), that the host opens a different door revealing a goat (not necessarily Door 3), and that he gives the player a second choice between the two remaining unopened doors.

Solution

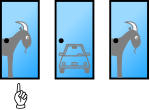
The overall probability of winning by switching is determined by the location of the car. According to the problem statement above, a car and two goats are arranged behind three doors and then the player initially picks a door. Assuming the player's initial pick is Door 1 (the same analysis applies for any other door the player picks):

• The player originally picked the door hiding the car. The game host must open one of the two remaining doors randomly.
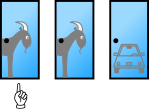
• The car is behind Door 2 and the host must open Door 3.
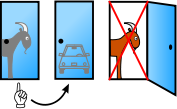
• The car is behind Door 3 and the host must open Door 2.

Players who choose to switch win if the car is behind either of the two unchosen doors rather than the one that was originally picked. In two cases with 1/3 probability switching wins, so the overall probability of winning by switching is 2/3 as shown in the diagram below. In other words, there is a 2/3 chance of being wrong initially, and thus a 2/3 chance of being right when changing to the other door.

Car hidden behind Door 1		Car hidden behind Door 2	Car hidden behind Door 3
Player initially picks Door 1
Host opens either goat door		Host must open Door 3	Host must open Door 2
Switching loses with probability 1/6	Switching loses with probability 1/6	Switching wins with probability 1/3	Switching wins with probability 1/3
Switching loses with probability 1/3		Switching wins with probability 2/3

Source :
http://en.wikipedia.org/wiki/Monty_Hall_problem
Krauss, Stefan and Wang, X. T. (2003). "The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser," Journal of Experimental Psychology: General 132(1). Retrieved from http://www.usd.edu/~xtwang/Papers/MontyHallPaper.pdf March 30, 2008.